Just How Accurate is Expected Goals?
In recent years, expected goals has become an increasingly important part of football analysis. As a measure of the quality of shooting chances that a team creates, expected goals claims to do a better job of showing how well a team played rather than how many goals they scored. Huge media outlets such as Sky Sports have started carrying expected goals as part of their routine match facts, alongside basic measures like possession and shots on target. On social media, debates over a team’s performance often revolve around the measure of expected goals. Since it has become such a household item among football fans and analysts, there’s one question that needs to be answered: just how accurate are expected goals?
What is Expected Goals?
Before diving into any numbers, it’s important to define expected goals and its uses. Put simply, expected goals (or xG, as it’s commonly known) is the probability (measured from 0 to 1) of a shot being scored. A shot with an xG of 0 would never result in a goal, a shot with an xG of 1 would result in a goal every time that a shot is taken. A shot with an xG of 0.5 would be scored 50% of the time. Perhaps the simplest way to illustrate the use of expected goals is for penalties. In professional football, roughly 76% of all penalties are scored. That means that any given penalty will have an xG of 0.76, because 76% of all shots taken from that situation will result in a goal.
Penalties are a useful tool to explain the probabilities involved in xG, but penalties are also an oddity in football because they are taken from the same spot and with the same conditions around them every single time. The success rate of penalties was known for a long time before xG came along. Where xG is most useful is that it can quantify the probability of any shot ending up in a goal, even in fluid situations like a counter attack.
Every shot that is taken in a game of football is compared to thousands of other shots taken from a similar position and is then assigned a probability of scoring. Because of the information gathered from the previous thousands of shots taken from a similar position, it is possible to work out the probability of a shot becoming a goal. If 1000 shots from position X has resulted in 100 goals in the past, a shot from that position has a goal probability of 10%, or an xG of 0.1. A shot from 30 yards from goal is going to have a very low xG (close to 0), while a shot from 2 yards out is going to have a very high xG (close to 1). Expected goals is therefore a way that the quality of the scoring chances that a team creates can be quantified. It can differentiate between shots taken in different situations; a striker shooting when 1v1 with the goalkeeper is clearly very different than a player shooting from 30 yards out, but traditional metrics like number of shots treat these equally. Expected goals is able to differentiate between different shots, enabling us to see the likelihood of goals resulting from the chances that a team creates. For a more detailed explanation of how xG works, and some of the edge cases, read more here.
How is xG used?
xG is used by teams, analysts, and fans alike to understand the underlying performance of a team. Because of the extremely low-scoring nature of football (the Premier League has averaged just 2.7 goals per game since 2017), outcomes are extremely random. Just one random event is enough to swing a football game from one team to the other. No single game has enough goals - or shots - to overcome randomness. While match outcomes will always remain the most important thing, a teams’s general performance is also important, and goals scored/conceded on its own is not sufficient to understand a team’s performance. That’s where expected goals come in.
To highlight the additional insight that expected goals can provide, let’s look at Manchester United’s 0-0 draw with Watford in February. Using the scoreline alone, one would conclude that Watford defended well to keep a clean sheet against a better team and that Man United did not play well enough to score against a weaker opposition. The outcome was a great draw for Watford and a disappointing draw for United. However, this was a match defined by poor defending by Watford and missed chances by Man United, which xG can show: United created 2.9 expected goals while Watford created just 0.5. So, while the outcome was certainly good for Watford, their actual performance was not. Randomness went in their favour on that day, with Man United managing to spurn countless great goalscoring opportunities. For United, despite a disappointing result, it is a sign that if that performance level is repeated, they would likely win a lot of matches.
What expected goals does is allow us to see more about a team’s performance than just outcomes, which is more likely to be a good predictor of their future results. Expected goals are often used to understand how sustainable a team’s results are. If a team has won 3 matches in a row despite creating very low xG, the idea is that those good results are likely an anomaly and won’t continue. Similarly, if a team has won 3 games in a row and created much more xG than their opposition in all three matches, their good form should be expected to be sustained in the long term. Because expected goals overcomes randomness, it should (in theory) be a more stable metric on which to base our expectations of a team’s upcoming matches.
This Sounds Great!
By this point I have spent a lot of time talking about why xG is useful, but it’s certainly not perfect. Expected goals is entirely based on measuring the likelihood of a shot becoming a goal - but what about attacks that don’t end in shots? As anyone who watches football knows, there are plenty of times in each game where a team might work the ball into a great position but don’t manage to shoot. Maybe a cross is just out of reach for a player, or maybe a defender makes a great last-ditch tackle before a shot can be taken. There are other scenarios, too, where xG might not fully take account of a team’s good play. If a team scores a goal that is ruled out for offside, that would not be counted under expected goals because the shot was not legal. But that doesn’t mean that the team should get no credit whatsoever for creating that chance - in some cases a player can be offside by the tightest of margins, meaning that the team still created a great chance even if a a player being offside by a few inches meant that it was disallowed.
Expected goals also doesn’t take into account who takes each shot. Football clubs around the world spend hundreds of millions of pounds every year to buy the best players, with the biggest fees being paid for attacking players - surely, Harry Kane has a much higher chance of scoring any given shot than Harry Maguire. That isn’t accounted for under expected goals.
With these potential issues in mind, I set about exploring whether expected goals are accurate.
The Numbers
To analyse the accuracy of xG, I used data available from FBRef, a website that tracks and stores statistics on teams, players, and matches. I exported information from FBRef - including the teams, scoreline, and expected goals - of every Premier League match since the start of the 2017/18 season until February 27th 2022, for a total of 1,776 matches.
First, I looked at the number of goals scored and the number of goals expected to be scored as measured by xG. In total, xG predicted that 4,692.1 goals would have been scored in the 1,776 matches, and in reality there were 4,858 goals scored. That is a difference of just 165.9 goals in nearly 1,800 matches. On a per-match basis (dividing the total difference by the number of games played), that means that xG predicts roughly 0.093 less goals to be scored than actually are scored. That is a phenomenally accurate result and shows how well xG does at predicting the actual goals scored in premier league matches. This result surprised me; because of the omissions that I mentioned above such as not counting attacks that don’t include a shot, I expected xG to under-estimate the number of goals scored. While the predicted goals were slightly less than actual goals, the difference per game is almost non-existent.
So on a simple count, xG does appear to be very good at predicting the number of goals scored over a large sample size. But there are other ways that we can test its accuracy. Let’s look at how well xG predicts the outcome of individual matches. As outlined above with the Man United vs Watford example, xG might not be so well suited to understanding who would win one single game.
To do this, first we have to decide the expected outcome (xOutcome) of a match according to expected goals: home win, draw, or away win. We have to define a difference between each team’s xG that means that the expected outcome would be for a team to win rather than draw. Because draws happen in football, we cannot simply say that if Team A has a higher xG than Team B, the expected outcome is for Team A to win. An xG difference of 0.1 would imply a draw is likely, while an xG difference of 2.5 implies that the Team A should win. For this analysis, I set this difference to 0.75. That means that if one team’s xG is 0.75 or more higher than the opposition, the expected outcome is for them to win, and if the difference between the two teams’ xG numbers is less than 0.75 the expected outcome is for a draw. 0.75 is, as any number would be, a somewhat arbitrary choice. Requiring a difference of 1 xG to say a team deserves to win feels too high, which would lead to so many expected outcomes being a draw. 0.5 was considered, but especially in games with high total xG it could be too small a gap to definitively say whether one team was expected to win over the other.
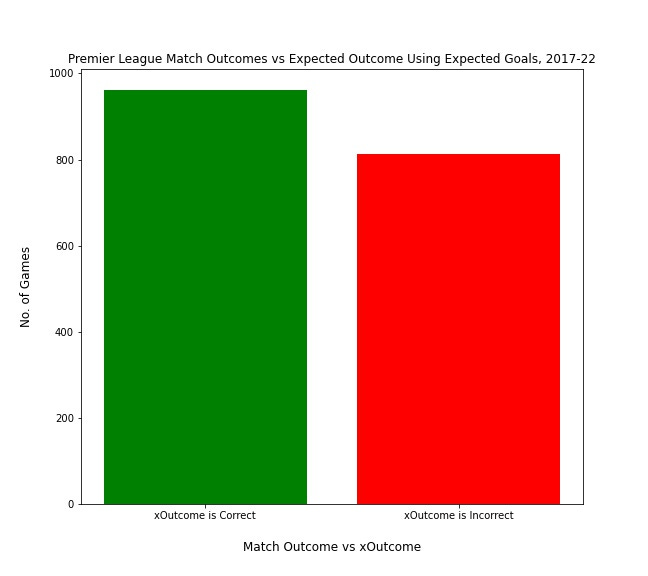
Using this definition of expected outcome, I calculated the percentage of games since 2017/18 in which the expected outcome was the same as the actual outcome. The results are shown in the graph below.
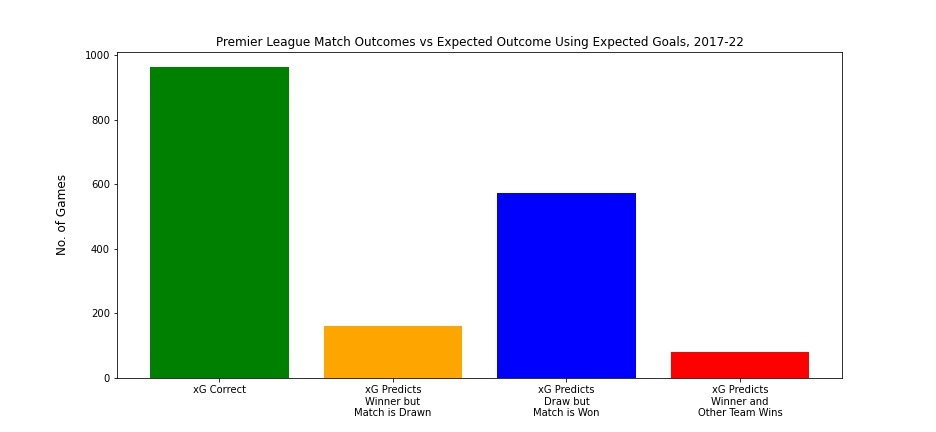
As you can see, the accuracy of expected goals is much less when looking at its power to predict single games. Football is such a random sport that, in one-off games, underlying performance may not be a particularly good judge of who wins. Not all failures to accurately predict the outcome of a match are created equal, though; it is worse for the expected outcome to be a home win and the actual outcome to be an away win than it is for the expected outcome to be a home win and the actual outcome be a draw. To look at which types of errors xG is making, the following graph shows in further detail where xG is going wrong.
This graph shows that, when xG does not correctly predict the outcome of a match, it is most common for it to predict a draw but for the match to be won by either team. Thinking about the nature of football, this is perhaps unsurprising: draws are a relatively rare occurrence, with only 23% of Premier League games since 2017 ending in a draw. The fact that so many games are decided by fine margins, and often by one goal, means that it’s not entirely surprising that xG is often predicting a draw (meaning that both teams performed similarly to each other) but one team comes out as the winner. What is instructive, though, is how few games have a severe error; in just 5% of cases did xG predict a winner and that team ended up losing. What this graph tells us, then, is that xG is not a perfect predictor, but it is very rarely completely wrong.
Not All Teams Created Equal
We have seen so far that xG is a very accurate measure of goals scored and a relatively good tool for predicting the outcome of certain matches. Until now, the numbers used have been aggregated among all teams in the Premier League. However, it’s also useful to see how the accuracy of xG changes on a team-by-team basis. To explore this, I created a new dataset with each team’s total goals scored and total xG since the start of the 2017/18 season, along with their average Premier League finish in that time. I then calculated each team’s ‘xG difference’ by subtracting the number of goals scored from expected goals to show the difference between expected goals and actual goals scored.
Upon first look at the results, there was significant variation in the accuracy of xG. The range of goals scored minus xG was from 54 to -19, a large variation considering the overall accuracy that expected goals has to predict total goals. This suggested that expected goals may be performing differently when predicting goals for certain teams than others. To find out, I plotted xG difference against average league position, with league position on the y-axis and goals scored minus xG on the x-axis. Teams towards the bottom of the graph have finished higher in the league (finishing first every year would give an average league position of 1). There is also a vertical dashed line at 0 xG difference. This indicates that a team scored exactly how many goals xG predicted. Teams to the right of this line over-performed their xG (scored more than expected), teams to the left of the line under-performed their xG.
The graph provides a few interesting insights. Firstly, there is an incredibly strong correlation between league position and xG difference (correlation of -0.86). This means that as teams finish higher up the Premier League table, the more that they outperform their expected goals. This finding somewhat makes sense, given that teams that finish higher up the table are likely to have the best players. That not only means that they are likely to create more chances, but you would also expect them to score more of the chances that they do create. That is exactly what this graph shows: the quality of chances created being equal, better teams score more of the shots that they take.
What is perhaps more surprising and interesting from this graph, though, is the amount of variation away from the line of best fit. The line of best fit (represented by the diagonal blue line on the graph) shows the general trend that is present in this dataset. It shows the expected difference between xG and goals scored at each average league position. The trend is that as league position improves, the more likely a team is to outperform their xG. However, at all average league finishes, there are a number of teams that differ significantly from the general trend.
Chelsea and Wolves are two teams whose results stick out; Chelsea have an average league finish of 3.8 and an xG difference of 12.7. Given the performance of other teams in this dataset, a team with an average league position of 3.8 would be expected to have an xG difference of around 40, a huge difference from Chelsea’s 12.7. Wolves, meanwhile, also significantly underperformed their xG compared to other teams that have similar average league finishes. The 95% confidence interval (represented by the shaded area of the graph) suggests that a team with Wolves’ league finishes (average of 8.75) would have an xG difference of around 15-25, whereas Wolves’ actual xG difference is minus 3.8.
Teams such as West Ham, West Brom, Stoke, Swansea, and Cardiff show the opposite problem, outperforming their xG more than you would expect given their league finishes. While West Brom, Stoke, Swansea, and Cardiff still scored less than xG predicted overall, their average league positions would suggest that they should have scored even fewer goals than they did based on the chances that they created. In total, 16 teams out of the 28 fall outside of the 95% confidence interval, which is suggestive of the high amount of variation in xG difference vs league finish.
That was a lot of words and numbers, but what does the information presented by the previous graph actually mean? Firstly, it means that our expectations for how many goals a team scores based on their xG should be different depending on the quality of the team. If Manchester City and Watford both rack up an xG of 2.5 in every game that they play, in reality we should expect that Manchester City will actually score more goals. They might be creating the same quality of chances (which is what xG measures), but the conversion rate of those chances will be very different.
Second, while xG might do a very good job of approximating the number of goals scored in total by all teams in the Premier League, it does a much worse job of predicting how many goals each individual team will score. Man City, for example, have scored 54 more goals than xG predicted - across the four and a half seasons in this dataset, they have scored an average of 12 goals per season more than xG expected. That is a huge amount of goals that can equate to a very significant difference in points scored during the season. At the other end of the scale, Fulham scored 19 goals fewer than xG predicted in two seasons in the Premier League, equating to 8 goals less than predicted per season. The sample size that we have in this data is large enough to deal with any short-term volatility; this means that the differences between xG and goals scored are real and persist over long periods of time.
Third, xG is at its best when predicting the number of goals scored by the average team in the Premier League. The whole idea of xG is that the chances of any shot going in is based on the conversion rate of thousands of similar shots in the past. It makes sense, then, that the overall xG probability is the average probability of a shot from a certain location going in. As a result, xG will be most accurate at predicting the goals scored by players of average ability, likely to be concentrated in average-performing teams. xG is less accurate the further you go from average performance; this is why you see teams like Manchester City at one end and Norwich at the other with large differences between their xG and actual goals scored. While xG’s total number of predicted goals might be very close to the total number of goals scored, when you break it down by team there are serious variations. The deviation from xG in both directions (both under- and over-performing xG) balances out when you look at the league as a whole, but within that overall accuracy there are some hidden flaws in xG’s predictions.
Put simply, what this data shows is that the best teams require less xG to score a goal. In normal terms, that means that they need to create less chances per goal scored. This is not a particularly revolutionary concept, but seeing it show up so vividly in data that is supposed to accurately depict a team’s performance is illuminating. xG is a wonderful stat to show us a team’s underlying performance, but how we extrapolate from there should be different based the team in question. In many ways, these results seem to present a double edged sword for struggling teams; not only will they likely create few chances (generating little xG), but they will also likely score a lower percentage of the chances that they do create. Perhaps there is some merit to the top clubs spending huge money on top strikers, after all.
View the code that I used in this analysis here.